Language: Python —
Full Code on Gitfront.io — https://github.com/cswartzell

A friend of mine is working on a Unity project based on faithfully recreating tabletop RPG rules, and asked for a hand coding the rules for movement. In Dungeons and Dragons character movement is done on a grid of squares where each square represents 5’ x 5’ of space. Traveling orthogonally from one square to another simply takes 5’ of movement. However, the rule for diagonal movements are… unusual.

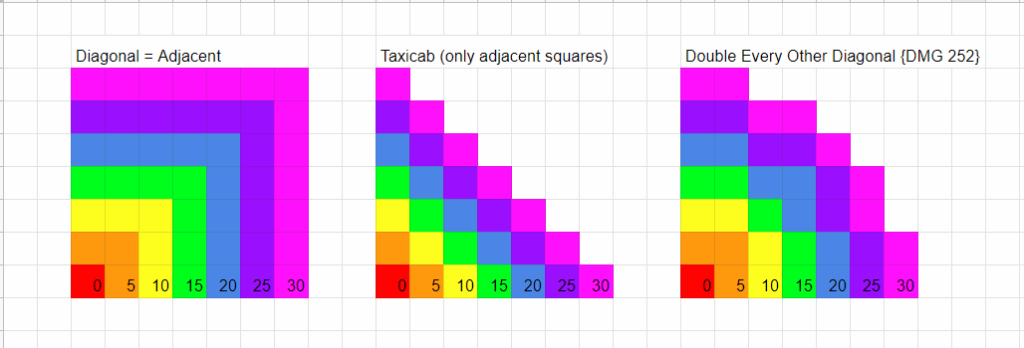
A character taking their first diagonal step in a turn is charged as having moved 5’. This makes all 8 squares surrounding the starting position an equal 5’ away. Afterwards, any second diagonal move during a turn takes 10’ of movement even if not contiguous or in the same direction as the first diagonal step. The pattern then repeats; 5’, 10’, 5’, 10’… simple enough and a good compromise for efficient movement on a grid. Plotting say 30’ of movement using this system starts to roughly approximates a circle.

As a coding challenge, how do we plot a characters movement? How do we draw a movement “circle” indicating grid spaces they can reach within their movement distance? How far away is a target from a character, assuming the most direct route using these movement rules?

As this project is Unity based, some simple solutions come to mind. My friend easily created a coordinate based grid system, and can arbitrarily assign scales to the world. We could simply take an actual measurement from the center of one grid position to another to determine their distance by rounding to the nearest 5’. Will this accurately model the rules though? Hard to say, but my intuition is it will accumulate errors, or rather “corrections” that deviate from the more approximate game rules vs real measure. Similarly, we could treat each diagonal move as 7.5’ and, again with rounding, come up with a decent approximation. While fine choices for a game these methods may not exactly match the game rules.

Instead, we need to come with an algorithm for determining optimum grid movement given the movement rules as written. The most efficient movement is orthogonal; moving in a straight path along a row or column always costs us 5’ per square. We want to travel in an orthogonal path toward our target for as much distance as possible. For any square not in our current row or column we will have to alter our direction at some point. However, unlike in real life, the straight line from the origin to the target may not be the shortest route if it costs an extra 10’ diagonal step we could have avoided.

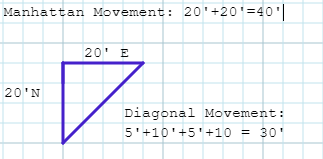
The least efficient movement would be L shaped, barring intentionally indirect paths. Using this method moving 4 squares North followed by 4 squares East would be 8 steps. Let’s start using coordinates to notate this; (0,0)->(4,4) at 5’ step size would be a “Manhattan Distance” of 40’. We could instead make just 4 diagonal movements NE to go directly toward the target. At a cost of 5’, then 10’, 5’ and 10’ again, we would arrive at the same square using only 30’ of movement. Diagonal movement is the more efficient than L shaped movement.

So, we want to travel in a straight line as much as possible yet may need to get over a few rows or columns first in order to do this. Combining these two ideas we see that we should move directly diagonally, along the shorter leg of the L, toward either the row or column that lets us make the rest of our movement in a straight line.

After some thinking and tinkering I hit upon the algorithm that solves this. Let’s call East-West movement row based and North-South column based. To go from our characters origin (0,0) to our target (tgt_row, tgt_col), we could travel the L shaped Manhattan Distance of (5’ * tgt_row) + (5’ * tgt_col) less some savings by moving diagonally. Specifically, we save 5’ of movement on the Manhattan route per odd diagonal step we take. We need to take diagonal steps for the minimum between tgt_row and tgt_col to get into a lane where the remainder of our movement is straight. Putting it all together, the most efficient route from one space to another using these rules is given by:

#Our target (x,y) is the absolute value of the offset from the characters position to the target’s step_size = 5 tgt_x = abs(char_row - tgt_row) tgt_y = abs(char_col - tgt_col) distance = step_size * (tgt_x + tgt_y - ceil(min(tgt_x, tgt_y)/2))

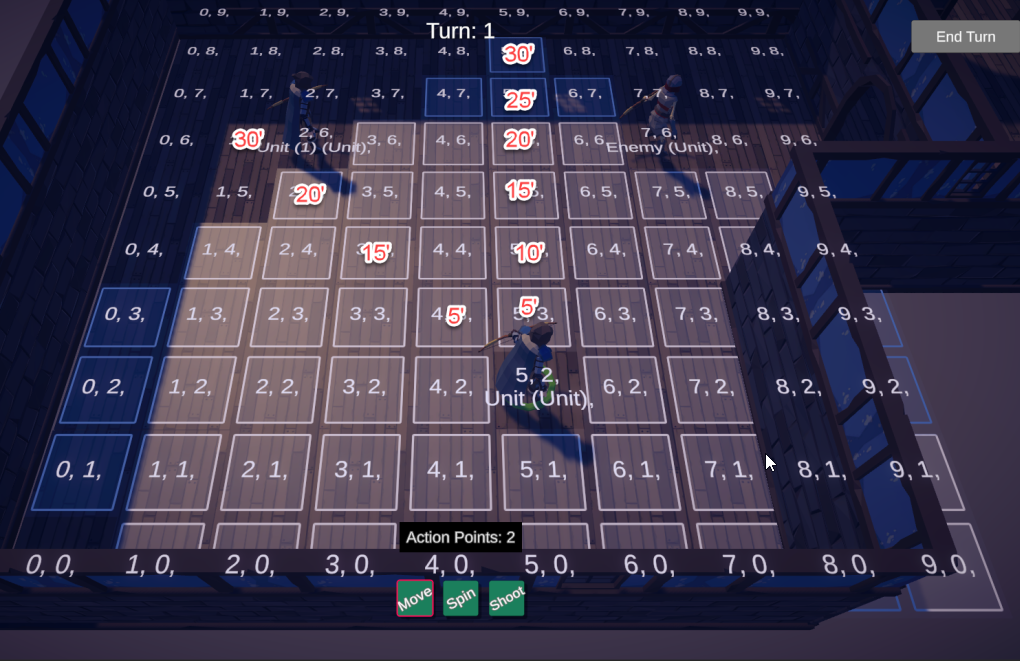
Using this as our basis, we can draw out a grid for movement costs on an arbitrary grid:

Limiting the output to our characters movement speed, we can correctly highlight the spaces our character can reach in a single move. We can also assign a target to a grid position (noted here by being underlined, and use the same formula to calculate the distance to a target:

Neat.