Category: Exploration

July 12th, 2023: Blackjack

Cameron SwartzellLeave a comment

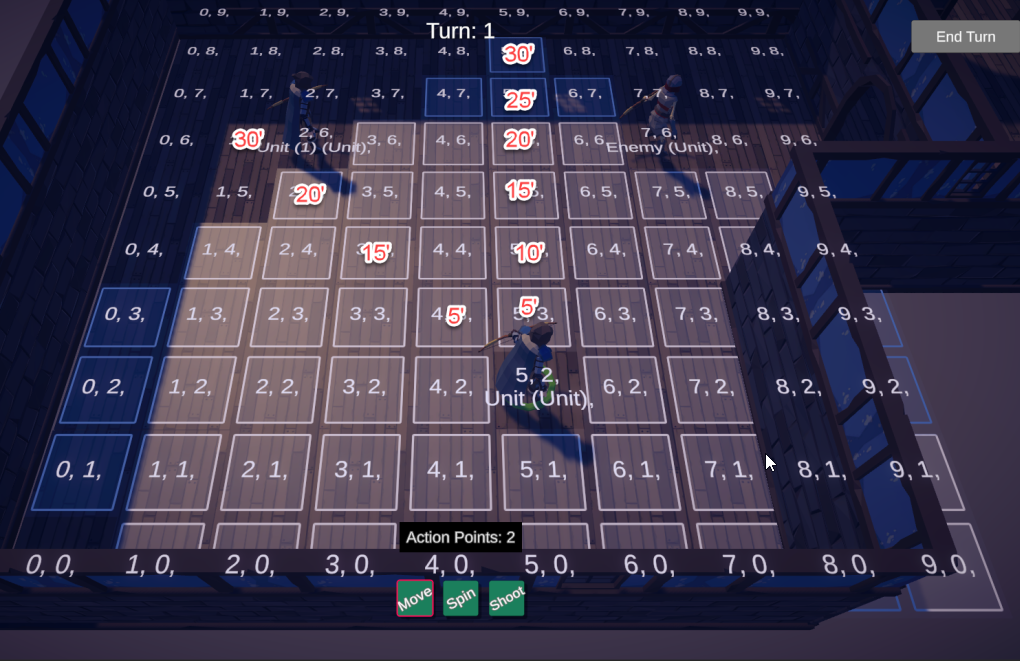
Today I challenged myself to write a simple console based game of Blackjack “In One Hour”. Several hours later and I’m done! It wasn’t so much that it was a tricky feat, rather I got hung up on a few areas of interest.

First, I discovered that the console (Windows in this case) supports UTF-8 by default, and all 52 standard cards actually do have their own printable character, neat! So I started playing with that for a while. First issue is the Unicode characters for cards look like this:

🂷🂬

So… quite unreadable. Ah well, at least I can just use the characters for suits (â™ , ♥, ♦, ♣) and draw my own old school ASCII art to display them. Oh wait, the “10” card is the only one to use two characters for its rank. Hmm, is there another character I could use? I could use the “enclosed numbers” block so it would be â‘©, but that looks weird if I don’t do them all and they are pretty hard to read too. Then I looked into combining characters which is a standard way of using Unicode and went down a few rabbit holes before deciding, as I’m sure many frustrated fussy hobbyist programmers before me have, that “T” is good enough to mean ten and move on having wasted a bunch of time.

When playing with the Unicode cards, I also noted that I was never seeing kings come up and couldn’t figure out why. It looked like an Off By One type error, but the rest of the program worked as expected. Turns out, Unicode includes an “alternate” rank called a “knight” that was used in France and Spain in times of yore. Now, obnoxiously dropped in the middle of the Unicode ordering. Fine, we can just add an offset to ignore this issue.

I also spent some time refamiliarizing myself with methods of randomizing and distributing elements from a collection and looked through the documentation of the random package in Python. I ended up writing my class for creating a deck, shuffling, dealing, and storing card information as I can reuse parts for future projects, but it was still informative learning some existing options.

Lastly, I spent a while just playing with timing and “animating” the game, such that it can be in console. Just blanking the console and reprinting various states. I could have been a bit more clever and stored sections in some sort of display buffer, only then editing the changing parts, but instead just wrote a few multipurpose, hard coded display sections which work well enough for a silly task like this.

Overall a fun little short project. Pretty simple, but not trivially so. Upon completing the base game, I decided to add doubling down on your bet as an option, which was simple enough. Now it all functions as intended, looks “good”, and is fun. Yet to tackle is Splitting as it’s a whole other display rigmarole I’ll have to deal with. It’ll bother me if I leave it unfinished though, so surely I’ll go back to it.

See Source Code on Github: https://github.com/cswartzell/SpeedRound.git

Hooray! It works!

Code Snippet

       def print_hand(hand, hide_first):
            for _ in range(len(hand)):
                print("╭――╮", end="  ")
            print()
            
            for crd in hand:
                if hide_first:
                    print(f"│🜲\u2009│", end=" ")
                    hide_first = False
                else:
                    print(f"│{crd.unicode_suit}{crd.unicode_rank}│", end="  ")
            print()
            
            for _ in range(len(hand)):
                print("╰――╯", end="  ")
            print("\n")
            

        def print_state(player_cash, dealer_hand, player_hand, player_total, hide_dealer, won=0, msg="", d_total=0):
            system('cls')
            print(f"                                             Cash: ${player_cash}")
            if won > 0:
                print(f"                                                  +${won}")
            elif won < 0:
                print(f"                                                  -${won}")
            else:
                print()
            print("Dealer: ", end="")
            if d_total:
                print(d_total)
            else:
                print()
            print_hand(dealer_hand, hide_dealer)
            print(f"Player: {player_total}")
            print_hand(player_hand, False)
            if msg:
                print(msg)
            if won != 0:
                sleep(.5)
                print_state(player_cash + won, dealer_hand, player_hand, player_total, hide_dealer, d_total=d_total, won=0, msg=msg)

Accounting Mystery: Yep, 2^n gets really big

Cameron SwartzellLeave a comment

Language: Python — Time: 10 minutes
Full Code on Gitfront.io — https://github.com/cswartzell

A colleague of mine received a check today for some receipts they had turned in for reimbursement. They were surprised to find the total was quite a bit less than they were expecting. Specifically, according to their tracking sheet, they had turned in 20 receipts totaling $475.98 but received only $304.22: a difference of $171.76. They asked if me if I thought maybe a section of receipts had perhaps fallen out and weren’t added by the Accountant. Aha! We can solve this in just a few lines! Surely there can’t be that many combinations that add up to a specific value from a subset of values that are within two orders of magnitude from each other and the target sum right? And there are only 20 receipts to deal with, this should be simple.

Well… the Power Set of a given set of length n is 2^n so… there are a lot of combinations. 2^20 = 1,048,576 combinations of receipts to be exact. Still, pretty manageable. “I could probably write a 2d DP solution for this” I thought to myself as I instead lazily abused itertools to simply generate all the the sets of iteratively. It ran in under a second. Good enough, you know what they say:

“Premature optimization is the root of all evil”- Knuth

And the result?

Twelve! Twelve combinations of possibly missing receipts that might explain the discrepancy. Sure, out of over a million possibilities it seems small, but I was quite surprised. Thinking on it further, the individual prices are conveniently clustered in a range around 10% of the target total, so it makes sense that the overwhelming majority of the sums of around 10 of these receipts might be at least within the ballpark of the target after all.

We concluded that it didn’t really seem likely that most of the receipts went missing from the stack, but the mystery remains. The accountant swears they added up what was presented to them correctly. The obvious question (as yet unanswered) is “yes, but how many receipts were there?”

Dungeons and Dice: Is +1d4 or Advantage Better?

Cameron SwartzellLeave a comment

Language: Python — Time: 90 minutes with research
Full Code on Gitfront.io — https://github.com/cswartzell

Another problem inspired by a Reddit thread: In Dungeons and Dragons nearly all actions are assigned a “DC” (Difficulty Class), which is a target number you want to meet or exceed when rolling a single 20 sided die (1d20) to succeed. For instance, “roll better than 15 to climb this wall”. There are certain actions players can take can aid their fellow party members, giving them assistance for these rolls. The Cleric spell Guidance, for instance, adds an additional 1d4 to a players next d20 roll while Enhance Ability grants “Advantage” on a roll which allows a player to roll two d20 and keep the higher result. Both of these options give a player a minor edge, but in different ways. Given the choice, which is statistically superior?

A pretty simple probability problem, and a good chance to play around with the matplotlib library in Python. We can simply generate all outcomes (1d20+1d4, and max(2d20)), calculate the probabilities of each combination, create a running total for each result showing “chance of rolling at least X”, and graph the result. Matplotlib allows us to create a clean, simple graph in just a few lines of code:

The answer ends up being quite surprising: It depends on the “DC” of the roll we are intending!

Adding 1d4 mostly just adds a simple offset to a linear probability, while advantage changes the probability to being nonlinear. Graphing the two, we see the lines cross each other multiple times, though just barely on the left.

On the low end, if we must avoid rolling a one to succeed in some challenge, then obviously we should take the added die as the lowest roll for 1d20+1d4 is 2, while there is still a slim possibility of 2d20 each showing a 1 (a 1 in 400 chance). Above this minimum, rolling 2d20 with Advantage gains an edge for some time, and results in the range 3-17 are significantly more likely.

For middle values we see that the Advantaged roll is significantly more likely to roll “at least” those targets. At its peak, rolling with Advantage gives us a 75% chance of getting at least 11, while 1d20+1d4 has only a 62.5% chance to be at least as much.

At 18 the lines very nearly cross again, though Advantage retains an edge, there being 27.75% chance of rolling at least 18 with Advantage compared with 27.50% if rolling 1d20+1d4. After a DC target of 18 the added 1d4 takes the lead again, and is more likely to give you a higher total. Significantly, the added d4 allows a player to roll above 20 as the combined results go up to 24. We now see this is actually the reason why the added die is less favorable for most middle target numbers: there are more total results so the probability of any specific result is commensurately reduced.

So, which to use? We see now this is dependent on the target DC— a value known only to the Dungeon Master. Players don’t have perfect information when playing and can only make an informed guess. Experienced players may have a sense (10 is pretty standard, 15 is a hard task, 20 is quite a challenge), and can perhaps game the system by estimating what the DM has in mind, but the difference is fairly slight either way.

More Math:
2d20 with advantage:
Mean: 13.82
Deviation: 4.71

1d20+1d4:
Mean: 13 (simply: mean 1d20 + mean 1d4 = 10.5 + 2.5)
Deviation: 5.87

Dungeons & Dragons & Diagonal Movement

Cameron SwartzellLeave a comment

Language: Python —
Full Code on Gitfront.io — https://github.com/cswartzell

A friend of mine is working on a Unity project based on faithfully recreating tabletop RPG rules, and asked for a hand coding the rules for movement. In Dungeons and Dragons character movement is done on a grid of squares where each square represents 5’ x 5’ of space. Traveling orthogonally from one square to another simply takes 5’ of movement. However, the rule for diagonal movements are… unusual.

A character taking their first diagonal step in a turn is charged as having moved 5’. This makes all 8 squares surrounding the starting position an equal 5’ away. Afterwards, any second diagonal move during a turn takes 10’ of movement even if not contiguous or in the same direction as the first diagonal step. The pattern then repeats; 5’, 10’, 5’, 10’… simple enough and a good compromise for efficient movement on a grid. Plotting say 30’ of movement using this system starts to roughly approximates a circle.

As a coding challenge, how do we plot a characters movement? How do we draw a movement “circle” indicating grid spaces they can reach within their movement distance? How far away is a target from a character, assuming the most direct route using these movement rules?

As this project is Unity based, some simple solutions come to mind. My friend easily created a coordinate based grid system, and can arbitrarily assign scales to the world. We could simply take an actual measurement from the center of one grid position to another to determine their distance by rounding to the nearest 5’. Will this accurately model the rules though? Hard to say, but my intuition is it will accumulate errors, or rather “corrections” that deviate from the more approximate game rules vs real measure. Similarly, we could treat each diagonal move as 7.5’ and, again with rounding, come up with a decent approximation. While fine choices for a game these methods may not exactly match the game rules.

Instead, we need to come with an algorithm for determining optimum grid movement given the movement rules as written. The most efficient movement is orthogonal; moving in a straight path along a row or column always costs us 5’ per square. We want to travel in an orthogonal path toward our target for as much distance as possible. For any square not in our current row or column we will have to alter our direction at some point. However, unlike in real life, the straight line from the origin to the target may not be the shortest route if it costs an extra 10’ diagonal step we could have avoided.

The least efficient movement would be L shaped, barring intentionally indirect paths. Using this method moving 4 squares North followed by 4 squares East would be 8 steps. Let’s start using coordinates to notate this; (0,0)->(4,4) at 5’ step size would be a “Manhattan Distance” of 40’. We could instead make just 4 diagonal movements NE to go directly toward the target. At a cost of 5’, then 10’, 5’ and 10’ again, we would arrive at the same square using only 30’ of movement. Diagonal movement is the more efficient than L shaped movement.

So, we want to travel in a straight line as much as possible yet may need to get over a few rows or columns first in order to do this. Combining these two ideas we see that we should move directly diagonally, along the shorter leg of the L, toward either the row or column that lets us make the rest of our movement in a straight line.

After some thinking and tinkering I hit upon the algorithm that solves this. Let’s call East-West movement row based and North-South column based. To go from our characters origin (0,0) to our target (tgt_row, tgt_col), we could travel the L shaped Manhattan Distance of (5’ * tgt_row) + (5’ * tgt_col) less some savings by moving diagonally. Specifically, we save 5’ of movement on the Manhattan route per odd diagonal step we take. We need to take diagonal steps for the minimum between tgt_row and tgt_col to get into a lane where the remainder of our movement is straight. Putting it all together, the most efficient route from one space to another using these rules is given by:

#Our target (x,y) is the absolute value of the offset from the characters position to the target’s step_size = 5 tgt_x = abs(char_row - tgt_row) tgt_y = abs(char_col - tgt_col) distance = step_size * (tgt_x + tgt_y - ceil(min(tgt_x, tgt_y)/2))

Using this as our basis, we can draw out a grid for movement costs on an arbitrary grid:

Limiting the output to our characters movement speed, we can correctly highlight the spaces our character can reach in a single move. We can also assign a target to a grid position (noted here by being underlined, and use the same formula to calculate the distance to a target:

Neat.